参数曲线观测法是振动时效效果判定的最直观的定性判断方法。由振动力学理论可以将振动时效消除残余应力的系统简化为单自由度、有阻尼系统的受迫振动来分析,涉及到的几个参数为振幅、固有频率和共振带宽等。并有其相关表达式如下:
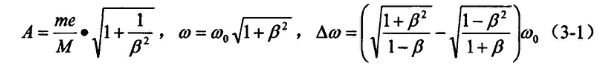
式中A为共振政府,m为偏心轮质量,e为偏心距,B材料结构阻尼系数,w为共振频率,w0为材料固有频率,△w为共振带宽。
由上式可以知道,阻尼的减小将导致共振频率的下降。在振动时效工艺中,阻尼会随残余应力的减少而下降,可得出工件的固有频率会下降,在振幅频率(A-F)曲线中表现为共振峰左移;阻尼的减少也将导致共振的上升和共振带宽变窄。图形表现为如下图所示:
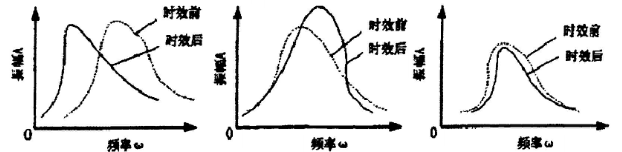
除了振幅频率(A-F)曲线能作为振动时效处理的判定依据外,振动时间(A-t)曲线也能作为判定依据。随着振动的进行,材料内部阻尼减小,振幅会随着增大。在振动处理一段时间之后,位错的移动越来越困难,阻尼的减少趋于稳定,振幅也会变得稳定。振幅随时间变化的规律因激振器的起振频率的取值范围不同也会有一定的不同,但是理论都是一致的。以三个参数振动频率fz,振后固有频率f1,振前固有频率f0作为参考,可得如下图所示的振幅时间关系图:
由振幅频率曲线和振幅时间曲线可得到低频振动时效参数曲线观测法的变化趋势如下:
振幅频率曲线振后相比振前:峰值升高,峰值点左移,带宽变窄;
振幅时间曲线在振动时效过程中:上升后变平,上升下降后变平,下降后变平 | 

 中文版 |
中文版 |  English
English








